Adaptive Detached Eddy Simulation of a High Lift Wing with Active Flow Control
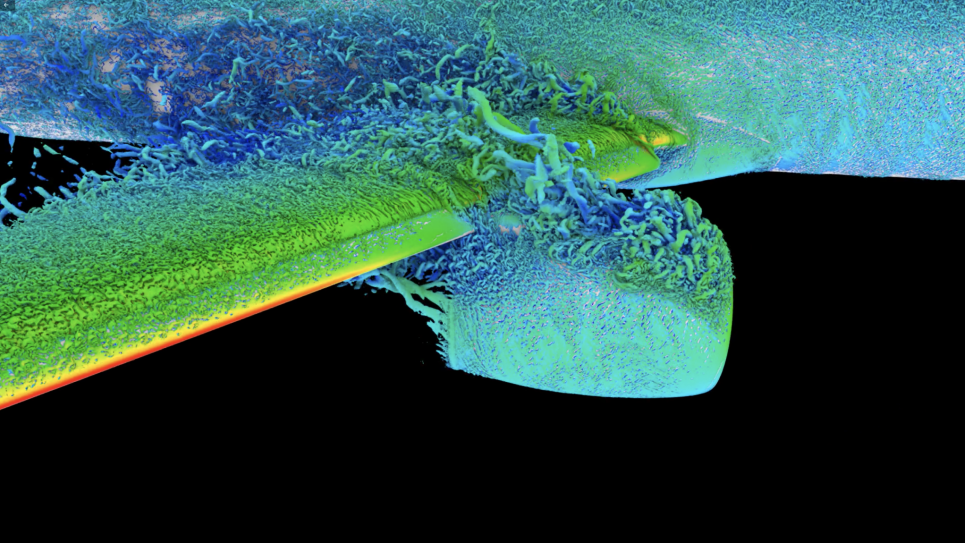
This project is economically motivated by the goal of redesigning control surfaces to reduce their size, thus reducing jet fuel usage at a cost-savings of approximately 0.3 billion dollars per year. With this INCITE award, researchers propose to develop adaptive detached eddy simulations of synthetic jet active flow control on a multi-component realistic high lift wing configuration. The simulations will provide fundamental insight into the interaction between synthetic jets and the main flow on a realistic geometry in aeronautics.
The team will model an array of synthetic jets that have been vectored to augment the stream-wise momentum near the flap suction peak, where separation is typically observed, to limit flap effectiveness for high-deflection angles and angles of attack. Simulations will allow for a fundamental study of flow control on a complex aeronautical control surface. The numerical simulations will provide a detailed view of the flow interactions as well as the insights required to understand and exploit the underlying physical mechanisms related to active flow control.
A secondary goal shows that the proposed baseline configuration is likely to become a reference for future simulations involving a lesser fidelity model, such as Reynolds-averaged Navier–Stokes (RANS) equations. Researchers will demonstrate that the recent developments in parallel adaptive meshing and parallel solver technology can yield fundamental insights into the complicated physics of flow control on real aircraft configurations.
The computational approach used for these simulations is the finite-element based flow solver, PHASTA, employed with anisotropic adaptive meshing and partitioning procedures. An excellent match to the active flow control simulations of complex and realistic wing configurations, these tools are applicable to flow problems that involve complicated geometries or complex physics.