Towards Ultimate Rayleigh-Benard Convection
Turbulent convection is an important area of research in fluid dynamics with applications to diverse phenomena in nature and technology, ranging from chip cooling devices and heat exchangers in power plants to convection in the Earth’s atmosphere, core, and oceans all the way to convection in the Sun and other stars. The turbulent Rayleigh-Bénard convection (RBC) model is at the core of all these turbulent flows. It can be studied in a controlled manner, but still has enough complexity to contain the key features of convective turbulence.
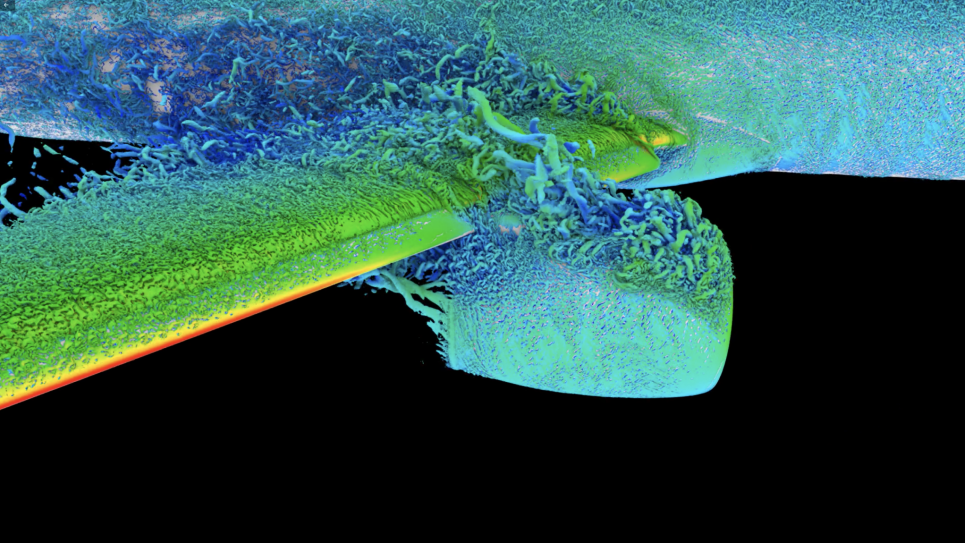
This INCITE project aims to shed light on the ultimate regime of convective turbulence in which the boundary layers become fully turbulent, resulting in significantly enhanced turbulent heat transfer. There are theoretical predictions and some recent experimental evidence of a possible transition into this regime, but three-dimensional simulations have not been able to capture the ultimate regime yet.
The research team will advance direct numerical simulations (DNS) to this new level of turbulence at Rayleigh numbers that have never been accessed before numerically. Their efforts are based on the Nek5000 spectral element software package, which was developed for solving flow equations on massively parallel supercomputers. In order to obtain the necessary high Rayleigh numbers of Ra ≥ 1016 for the ultimate regime at a Prandtl number Pr = 0.7, the researchers will take an unconventional step and study RBC in very slender cylindrical cells with an aspect ratio (diameter/height) of 1/10.
The team’s DNS will provide new insights into the global structure of the convection flow and into the details of the increasingly intermittent boundary layer dynamics. The data obtained in this project will also help to resolve the contradictory experimental results for the onset of the transition to the ultimate regime. Ultimately, the team’s study will provide a better understanding of the heat and momentum transport as a function of Rayleigh number. As such, their findings will be transformational in the domain of fluid dynamics with a variety of important applications.