Uncertainty Quantification for Turbulent Mixing
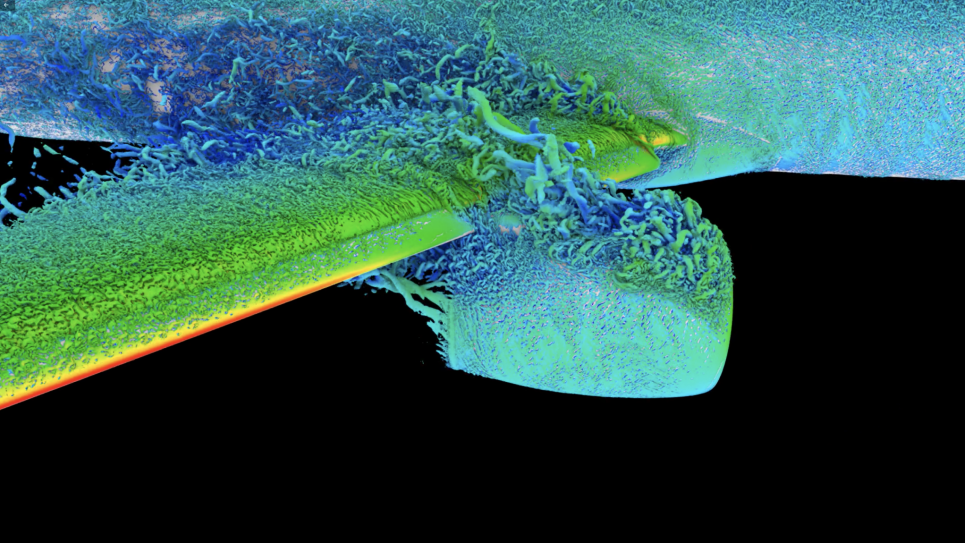
Rayleigh-Taylor (RT) unstable mixing flow challenges conventional ideas of computational science and sheds light on differing views for the computation of turbulent mixing flows. The problem is encountered in a variety of contexts, such as combustion, inertial confinement fusion, supernovae explosions, and geophysics.
Led by James Glimm of Stony Brook University, researchers are verifying and validating parameterized subgrid models for turbulent mass, momentum, and thermal diffusion that capture unresolved phenomena as it impacts coarse grid scales in a Large-Eddy Simulation (LES) having steep numerical gradients. Refined mesh simulations based on the front tracking algorithm, with INCITE allocations on Intrepid, the Blue Gene/P high-performance computer at the Argonne Leadership Computing Facility, resolve key length scales and minimize the role of models.
The front tracking method is an adaptive computational method that provides sharp resolution of a wave front by tracking the interfaces between distinct materials. It represents interfaces explicitly as lower dimensional meshes moving through a rectangular grid. The method has been implemented in the code FronTier, which solves the equations with the following steps:
- Interface propagation,
- Interpolation reconstruction,
- Interior states update.
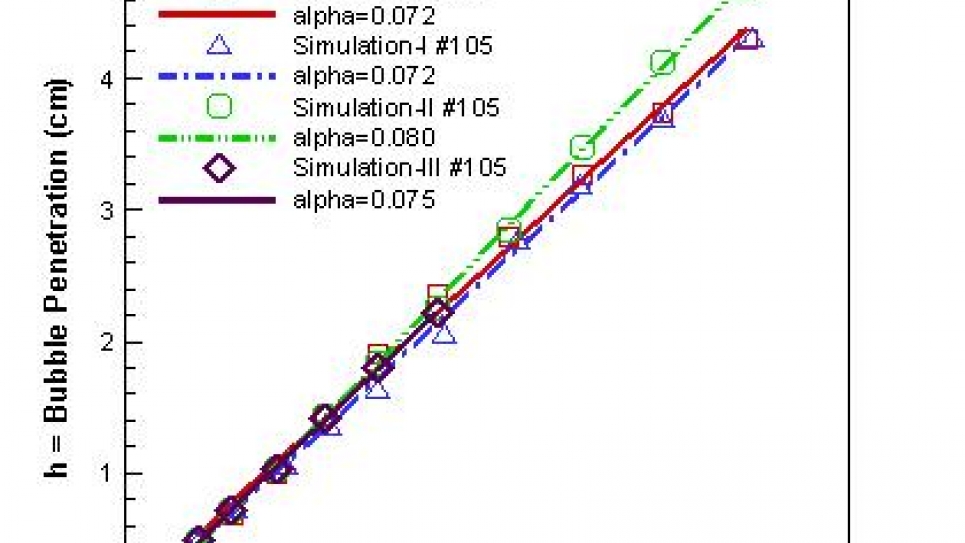
The problem is to predict the growth rate a, defined in terms of the penetration distance h of the light fluid into the heavy fluid via the equation h = α Agt2 , where A is the Atwood ratio, a dimensionless measure of the density contrast, and g is the acceleration, applied normal to an interface separating fluids of density ρ1 and ρ2.
The error estimates in the t = t0 reconstructed initial data are used to establish an uncertainty quantification interval for numerical simulations of the RT growth rate α.
- Maximum ±5% effect on the growth rate
- Agreement with experimental data of Smeeton & Youngs, 1987
- Resolution of critical length scales, to diminish and verify the role of models