An international research team, led by ALCF computational chemist Anatole von Lilienfeld, is developing an algorithm that combines quantum chemistry with machine learning (artificial intelligence) to enable atomistic simulations that predict the properties of new materials with unprecedented speed.

From innovations in medicine to novel materials for next-generation batteries, this approach could greatly accelerate the pace of materials discovery, with high-performance computing tools offering important assistance, or even full-blown alternatives, to time-consuming laboratory experiments.

This cutting-edge work is an example of how the ALCF aims to extend the frontiers of science by solving key problems that require innovative approaches and the largest-scale computing systems. Von Lilienfeld and his colleagues have made significant advances by running simulations on Intrepid, the ALCF's Blue Gene/P supercomputer, through a Director's Discretionary allocation (an in-house discretionary program that awards start-up time to researchers with a demonstrated need for leadership-class computing resources).

Here, von Lilienfeld sheds some light on where the research stands now and where it’s headed in the future.

This tool could result in a paradigm shift for materials design and discovery. Can you explain how this research could change the field?

We apply statistical learning techniques to the problem of inferring solutions of the electronic Schrödinger equation, one of the most important equations in atomistic simulation using quantum chemistry. Conventionally, this differential equation is solved with what we call the self-consistent field cycle, an algorithmic method that iteratively approaches the electronic wavefunction in which the potential energy of the system is minimal. The computational effort for this task is significant, and has historically resulted in a strong presence of quantum chemists at high-performance computing centers around the world. While this deductive approach is perfectly valid, it is frustrating that one has to restart the iterations again every time the chemical composition changes. Our approach attempts to infer the solution for a newly composed material instead, provided that a sufficiently large number of examples have been used for training.

What kinds of applications stand to benefit from this approach?

This approach is promising for any attempts to virtually design novel materials. In particular, when quantum mechanics and a substantial amount of screening is required.

Why are high-performance computers, like the supercomputers you’re using at the ALCF, required for this work?

Machine-learning techniques require very large amounts of data in order to infer solutions for interpolating scenarios with satisfying accuracy. Many thousands, if not more, data points are required. At such scale, it rapidly becomes unfeasible to obtain the data from experiment, and instead we have to rely on supercomputers to simulate such large numbers of materials.

Compared to existing research methods, how much faster could materials be developed using this algorithm?

For small organic molecules, we have observed speedups of several orders of magnitude. As one example, using density-functional field theory (DFT) to calculate a molecule’s atomization energy can take many minutes with one CPU. Estimating that same property with the machine-learning model would result in a prediction within milliseconds. For a fair comparison, however, the CPU time invested in generating the database for training has to be taken into account.

The electronic Schrödinger equation is one of the biggest obstacles to this computational approach. How were you able to work around the equation?

The Schrödinger equation’s solutions are complex, and it is not trivial to gain qualitative insights that go beyond its solution for the energy of a given system, and that enable us to transfer and reapply the insights to novel compounds. As such, machine learning offers a systematic and rigorous way to properly integrate the results from all the previous solutions into a single, closed mathematical expression.

Mathematically speaking, our machine learning efforts rely on the paradigm of supervised learning (i.e., given an equation and a large set of corresponding dependent and independent variables one can interpolate the dependent variables for new sets of independent variables). One of the challenges consisted of how to represent the independent variables that make up chemical compounds in Schrödinger's equation. We came up with a representation, dubbed the “Coulomb” matrix, to express the nuclear electrostatic repulsion between all the atoms in the system. It turns out that this representation is particularly well suited for the accurate energy interpolation towards novel chemical compounds that were not part of the training data set, so-called “out-of-sample” compounds.

In 2011, you organized and chaired a program at the Institute for Pure and Applied Mathematics (IPAM) at UCLA to advance research in the chemical compound space by overcoming bottlenecks. What motivated this effort?

From the atomistic simulation perspective, chemical compound space (CCS) is the set of all possible combinations of atom types and positions, each making up a “system” within Schrödinger's equation. A pharmaceutical chemist has a very different idea of CCS, basically consisting of all the possible graphs, vertices, and edges representing atoms and bonds, respectively. The materials scientist, by contrast, will typically define CCS in terms of crystal symmetries of periodically repeating unit cells that contain varying stoichiometries. Yet, one of the more important goals these scientific disciplines and many others pursue consists of finding novel compounds by navigating CCS. The applied mathematics program that takes place every year at the National Science Foundation-funded IPAM has had a remarkable record for bringing together very diverse communities in order to speak to each other as well as to applied mathematicians. IPAM's scientific board recognized the merits in realizing the proposed long-term program on “Navigating Chemical Compound Space for Bio and Materials Design,” and they provided invaluable assistance to make it happen. The program consisted of six one-week workshops with topics including a tutorial, mathematical optimization, physical frameworks, materials design, biodesign, and a culminating workshop at the UCLA conference center. The board was also crucial for establishing the links to many of the mathematicians who were interested in the topic, including my new collaborators from the Technical University in Berlin with whom I developed the machine-learning algorithms.

Can you explain how you demonstrated proof of principle with the algorithm?

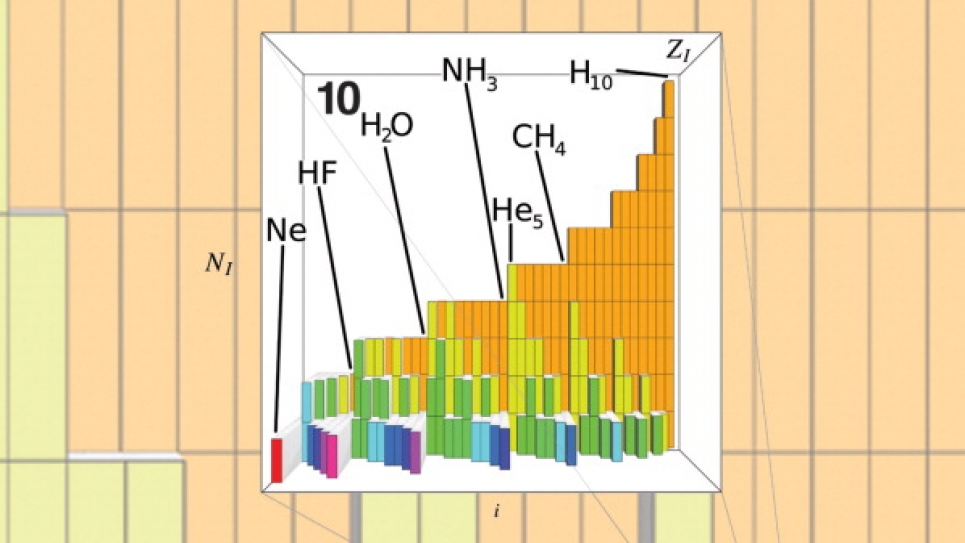
First, we had to generate the data. Using supercomputers such as Intrepid, the ALCF’s Blue Gene/P IBM machine, we solved well-known, and sufficiently accurate, approximations to Schrödinger's equation to obtain energies and other properties (dependent variables) for roughly 7,000 organic molecules (independent variables), which were proposed in an enumeration study by the laboratory of Prof. Jean-Louis Reymond at the University of Berne, Switzerland. Subsequently, we cast all the molecules in their Coulomb-matrix form, and we randomly divided the data into two sets: the training set and the testing set. We fitted the training set data with what is called a kernel-ridge-regression method using the Coulomb-matrices as variables. We used the resulting model to predict the properties of all the molecules in the testing set. The comparison of the predicted properties to the properties obtained from solving Schrödinger's equation was very good. We could furthermore show that as one increases the training set, the agreement of the test set results with the numerical reference results improve. Hence, we concluded that this is a practical approach to infer solutions of Schrödinger's equation for novel chemicals.

Some of your peers have also demonstrated proof of principle with other applications. Can you tell us what else is currently being done in this research space?

The idea of applying supervised learning to quantum mechanics has also been applied to learn energies based on electronic densities, rather than based on the Coulomb-matrix. This has great potential to arrive at much more accurate approximations to Schrödinger's equation than the approximation we used in our study, for example. A more conventional application, with the first papers appearing in the 1990s, consists also of using machine learning to infer energies for new geometries. This can be very helpful to speed up molecular dynamics calculations. These are used when all the atomic degrees of freedom of a given system have to be sampled for many steps so that one can apply the laws of statistical mechanics (i.e., allowing one to compute macroscopic properties of the material, such as thermal stability or phase diagrams). Other recent applications of machine learning to atomistic simulation rely on unsupervised learning of critical geometrical features, such as transition states of chemical reactions, or to detect relevant atomistic motion in biomolecules with many thousands of atoms.

Such interdisciplinary work as ours would not have been possible without my new collaborators from the machine learning group of Prof. Klaus-Robert Müller at the TU Berlin. When we first met, I challenged them on how to learn across different molecules to predict properties. Fundamental properties, such as the energy, can be calculated for any molecule using Schrödinger's equation. Consequently, it boiled down to learning this equation. At IPAM, we have spent many exhausting and late night hours trying to clarify our mutual ideas stemming from different backgrounds, and it was only after learning from many failed attempts that we managed to implement a successful model. Later this year, the first author of our study, Matthias Rupp who was a postdoc with Prof. Müller when we met at IPAM, will join my new group in the chemistry department of the University of Basel where we plan to build on these studies using the ALCF's resources remotely.

What are the next steps? How far away are we from seeing this become a widely used tool?

We are still at a very early stage where we need to better understand all the limitations and potential of this method. Mira, the ALCF's new Blue Gene/Q supercomputer, will certainly play a crucial role in generating the data sets with which we hope to perform the necessary studies. In two to three years, we will be able to give a more qualified verdict if this approach truly fulfills all the expectations.