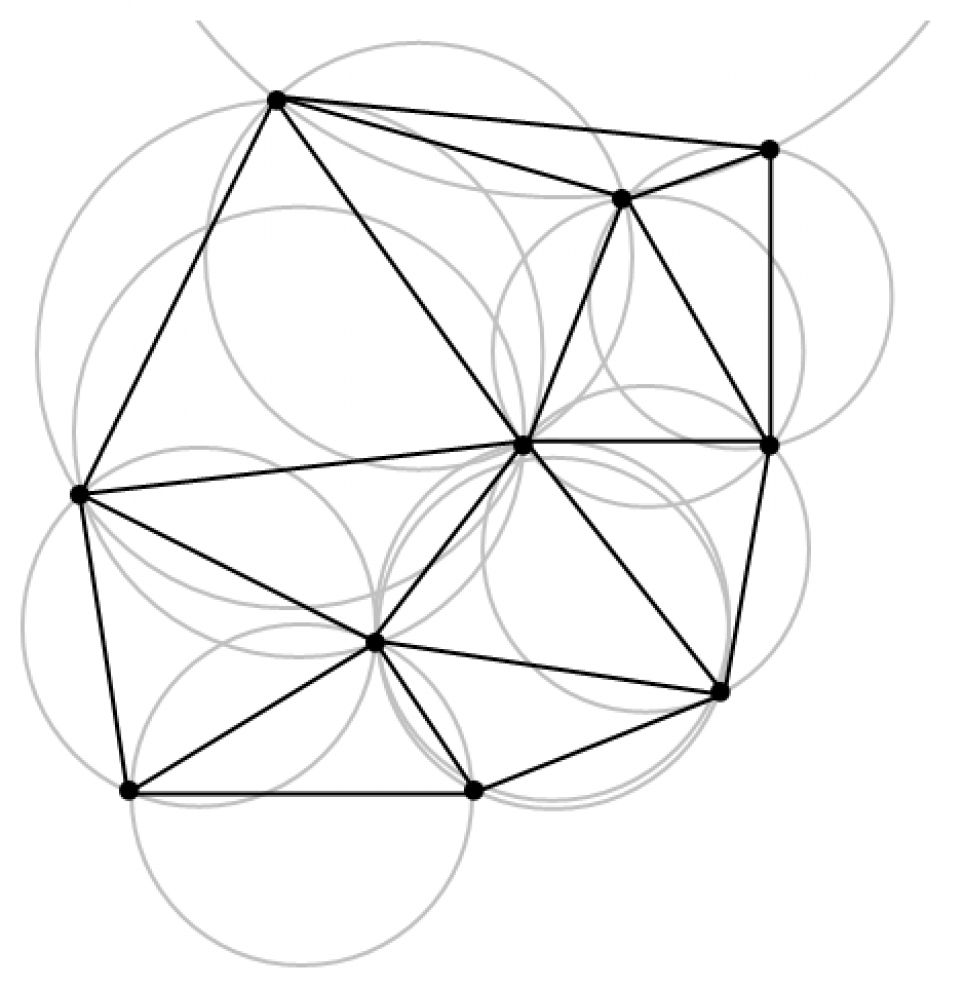
Abstract:   In this talk, two distinct problems in data-driven computational science are considered.  The first problem is the interpolation problem, where an unknown response surface representing an underlying phenomenon is approximated by finding a function that exactly matches available data.  To solve the interpolation problem, a novel algorithm is demonstrated for computing only a sparse subset of the elements in the Delaunay triangulation, as needed to compute the Delaunay interpolant.  For high-dimensional data, this reduces the time and space complexity of Delaunay interpolation from exponential time to polynomial time in practice.  The second problem is the multiobjective optimization problem, where the tradeoff surface (called the Pareto front) between multiple conflicting objectives must be approximated in order to identify designs that balance real-world tradeoffs.  In order to solve multiobjective optimization problems that are derived from computationally expensive blackbox functions, such as engineering design optimization problems, several methodologies are combined, including surrogate modeling, trust region methods, and adaptive weighting.  The result is a numerical software package that finds approximately Pareto optimal solutions that are evenly distributed across the Pareto front, using minimal cost function evaluations.  For each of the above problems, both serial and parallel implementations are described.