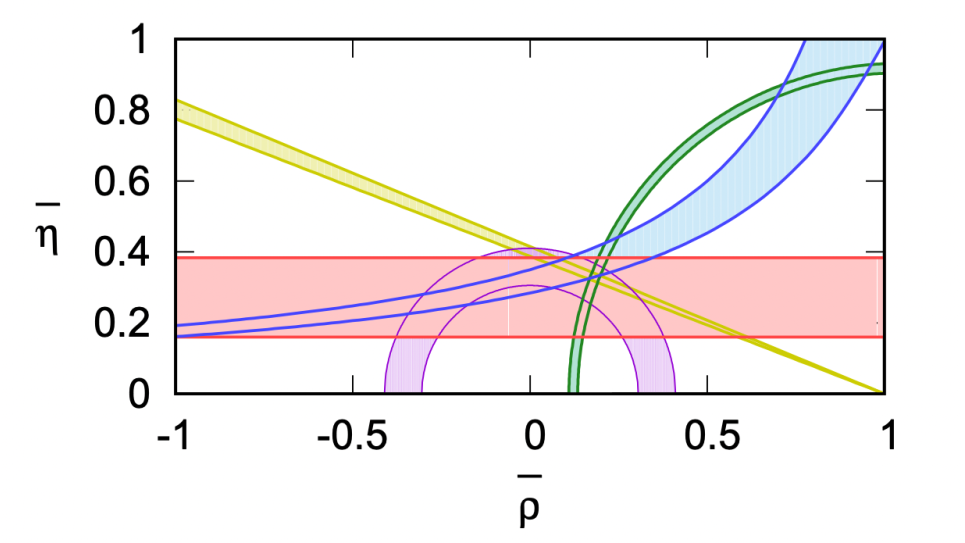
The constraints on the apex of the CKM unitarity triangle in the ρ −η plane. The pink band (ε 0 ) is the new constraint obtained through our calculation. The proposed research is a vital step towards reducing the error band by a factor of ten over the next decade.